고득점 Kit의 징검다리 문제를 부숴보자😒
안녕하세요! 두두코딩 입니다 ✋
오늘은 고득점 Kit 문제 중 징검다리 문제를 풀어보겠습니다.
🖇 소스코드에 마우스를 올리고 copy 버튼을 누를 경우 더 쉽게 복사할 수 있습니다!
궁금한 점, 보안점 남겨주시면 성실히 답변하겠습니다. 😁
+ 감상평 댓글로 남겨주시면 힘이됩니다. 🙇
문제
해당 문제는 고득점 Kit 문제 중 징검다리 문제입니다. 자세한 문제내용은 여기를 참조 부탁드립니다. (저작권 문제가 있어 부탁드립니다 🙇)
문제이해
(문제를 읽었다는 전제하에 글을 작성합니다! 🙄)
해당 문제는 처음 접했을 때, 이해가 바로 되지 않았다. 그래서 그림을 그려가며 무슨 문제인지 이해하려고 노력했다.
문제에서는 시작점이 “0” 이라는 점을 명시해주지 않고 돌 간의 간격이 나와있었다.
문제를 풀어서 생각해보면, 아래의 그림과 같이 표현할 수 있다.
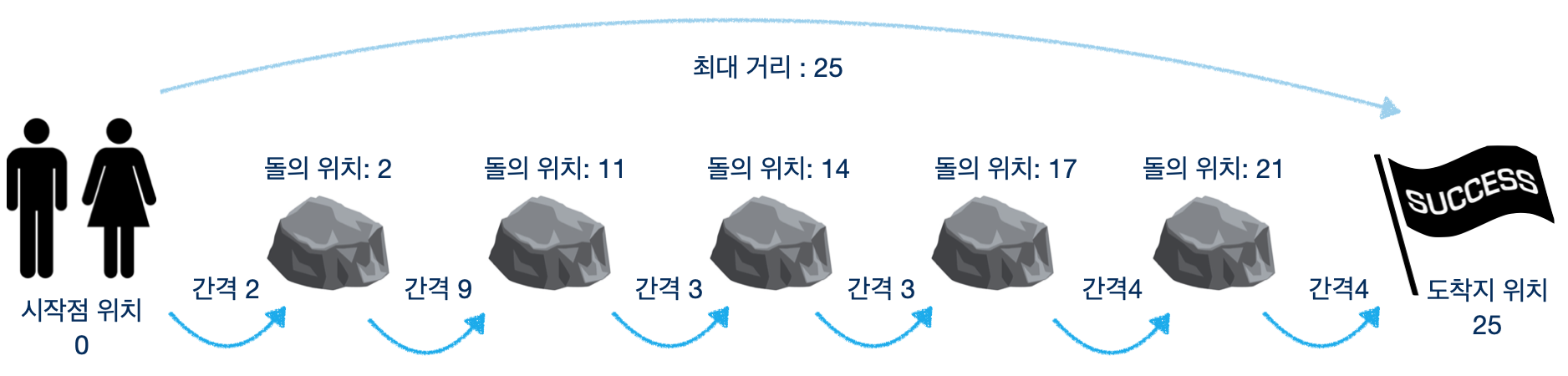
문제에서는 돌의 위치와 마지막 지점의 위치가 주어진다. 시작점은 0으로 가정을 하고 진행해야한다. (생각해보면, 거리가 음수가 될 수 없으니 당연한 것 같기도하고..)
무튼 0부터 진행하면, 최대거리가 25라는 값이라는 것을 알 수있다. 그리고 돌의 위치별로 정렬해서 생각해보면, 간격이 나오게된다.
이떄, 문제에서는 돌을 n개 뺏을 때, 나올 수 있는 최소값 중 최대값을 구해라 라고 한다.
즉, n개를 빼는 하나의 예시를 보면 아래와 같다.
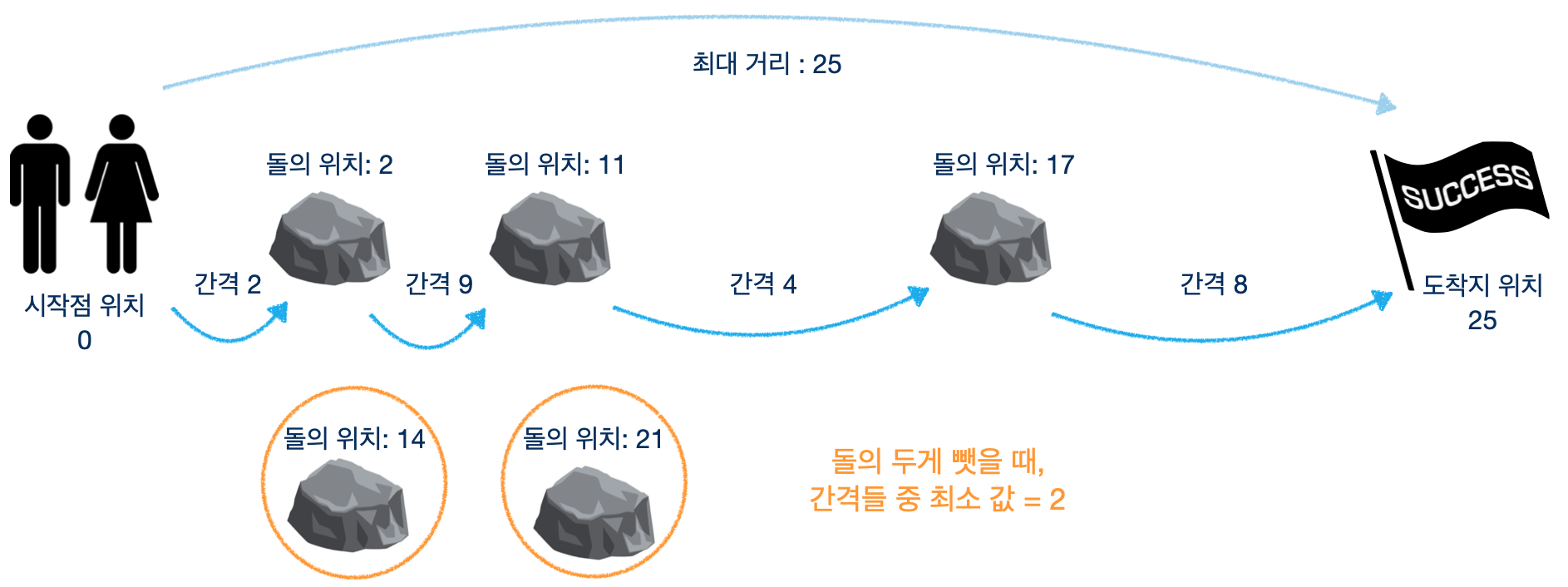
돌을 2개 빼야하는데, 14지점 과 21지점을 뺏을 때 최소 간격은 “2”라는 것을 알 수있다.
이렇게 n개를 뺄 때, 나올 수 있는 최소값들 중 최대값을 찾으면 되는 문제이다.
풀이
해당 문제는 이분 탐색을 활용해 풀 수 있다.
우선, 문제 자체가 이분탐색 카테고리에 들어가 있어서 당연하게 이분 탐색으로
풀어야지 라고 생각할 수 있다. 하지만, 문제를 구하는 답을 보면, 거리이고 거리가
1억과 같은 아주 큰 값이면 뭔가 “이분탐색”의 냄새가 난다..👃” 생각을 하고 접근하는 것이 좋다. (생활 속 꿀팁이다 😏)
접근 방법
해당 문제는 문제를 구하는 패러다임만 조금 바꿔서 생각하면 쉽게 풀 수 있다.
해당 문제는 “돌을 n개 뺏을 때, 나올 수 있는 최소값 중 최대값” 을 구해라라고 하는 문제이다. 마치 문제에서는 돌을 빼면서 모든 경우의 수를 다 구해라 라고 하는데, 경우의 수 다 구하면 뭔가 “시간초과” 날 것 같은 느낌이 든다.
해당 문제를 아래와 같은 문구로 변경해서 생각해보자.
“내가 찍은 최대간격에서 돌을 n개 빼고, 최소 간격으로 만들 수 있나?”
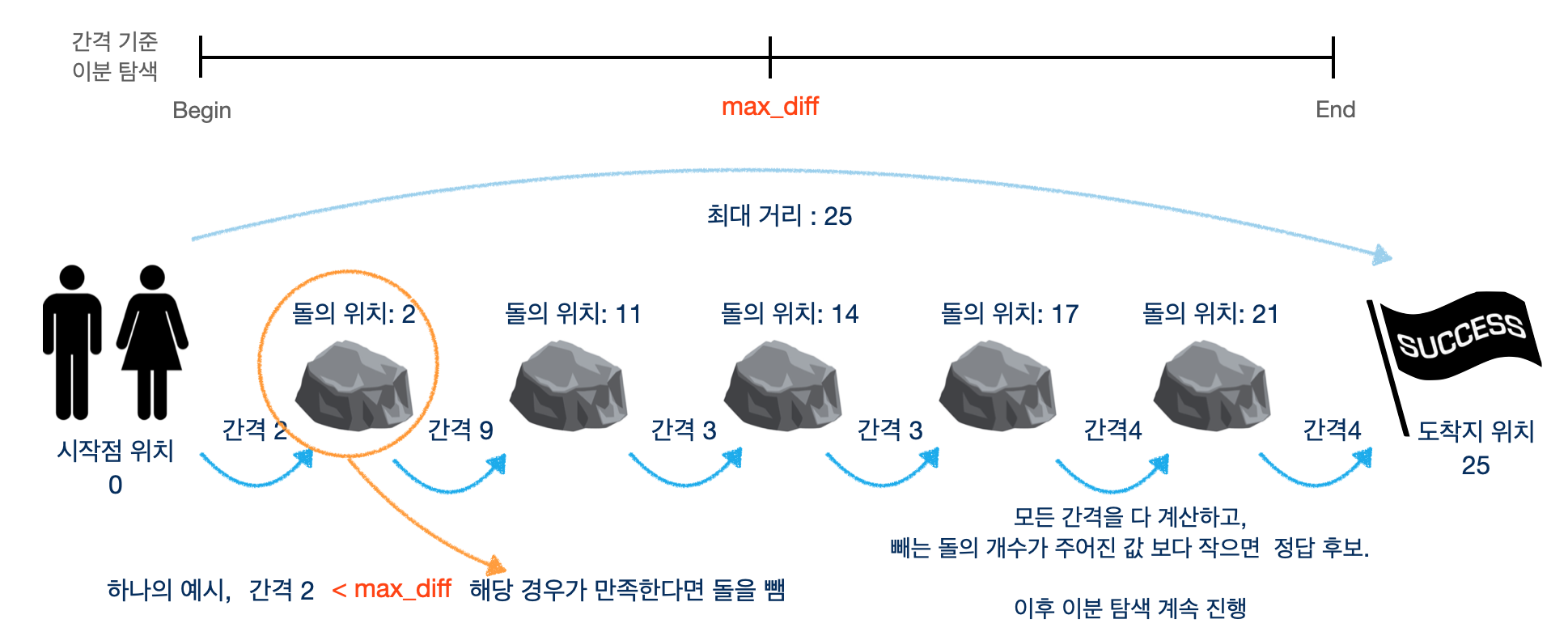
위의 예시 그림과 함께 보자.
우리는 최소로 건널 수 있는 거리가 1 최대로 건널 수 있는 거리가 distance - 1
이라는 것을 알 수 있다. 이 때, 거리기준으로 이분탐색을 진행하는데, mid 값을
현재 시점에 “최대간격”으로 생각한다.
해당 “최대간격”을 기준으로 현재 돌들 사이의 간격이 작다면, 돌을 뺀다. 돌을 빼게 되면 간격이 더 길어지게 되는데, 더 길어진 간격과 또 “최대 간격”을 비교한다.
위의 예시를 보면, 간격이 2일 때, 내가 이분탐색으로 찍은 최대값 max_diff보다
작은가? 를 확인한다. 만약 작다면, 해당 돌을 빼게 되고, 간격을 늘려준다. 지금
예시로 보면, 간격 2를 표현하는 돌이 빠졌기 때문에, 다음 돌과의 간격이 11이
되는 것을 알 수 있다. 이후 간격 11과 max_diff 비교하는 동작을 반복수행한다.
위의 동작은 내가 찍은 “최대값”이 돌들의 모든 간격 중 “최소값”이 되도록 한다.
“최소값”이 되도록 했을 때, 돌을 몇개 뺐는지 확인 하고, 주어진 인자 n보다
작거나 같은지 확인해 정답처리한다.
위 내용을 이제 소스코드로 구현해보자 🤓
소스코드
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(int distance, vector<int> rocks, int n) {
int answer = 0;
sort(rocks.begin(), rocks.end());
rocks.emplace_back(distance);
int begin = 1;
int end = distance - 1;
while (begin <= end) {
int prev_rock = 0;
int remove_stone_cnt = 0;
int max_diff = (begin + end) / 2;
for (auto rock : rocks) {
if ( rock - prev_rock < max_diff)
remove_stone_cnt++;
else
prev_rock = rock;
}
if (remove_stone_cnt <= n) {
answer = max(max_diff, answer);
begin = max_diff + 1;
} else
end = max_diff - 1;
}
return answer;
}
Appendix
주석을 추가한 코드이다.
모르는 부분이 있다면, 과감히 댓글을 남기자🤗
/*******************
제한사항
* 도착지점까지의 거리 distance는 1 이상 1,000,000,000 이하입니다.
* 바위는 1개 이상 50,000개 이하가 있습니다.
* n 은 1 이상 바위의 개수 이하입니다.
********************/
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(int distance, vector<int> rocks, int n) {
int answer = 0;
// 돌의 간격을 위한 내림차순 정리
sort(rocks.begin(), rocks.end());
// 마지막 포인트를 넣어줌..
// 소스코드 한줄을 줄이기 위함.
// 아래에서 간격을 구하는 부분이 있는데, 만약 넣지 않으면 if문 추가해야함.
rocks.emplace_back(distance);
int begin = 1;
int end = distance - 1;
// 이분탐색 진행
while (begin <= end) {
int prev_rock = 0;
int remove_stone_cnt = 0;
int max_diff = (begin + end) / 2;
for (auto rock : rocks) {
// 현재 내가 찍은 최대가 최소가 될 수 있는가?
if ( rock - prev_rock < max_diff)
// 간격이 짧으면 돌을 빼서 늘려줌
remove_stone_cnt++;
else
// 다음 돌의 간격을 구하기 위해 현재 돌 저장
prev_rock = rock;
}
// 주어진 n보다 빼야하는 돌의 개수가 작은지 확인
if (remove_stone_cnt <= n) {
answer = max(max_diff, answer);
begin = max_diff + 1;
} else
end = max_diff - 1;
}
return answer;
}
해당 부분에서 의문인게.. 문제에서는 n개의 돌을 무조건 뺴야된다는 것처럼 했는데, 만약 n개의 돌을 뺐을 때만 정답으로 처리하고자 하면 error가 뜨는 것을 확인할 수 있었다. 즉, n보다 작은 돌의 빼는 경우도 맞다고 처리하는 것 같다.. (문제가 이상한건지.. 내가 이상한건지..? 😵)


