고득점 kit의 가장 먼 노드 문제를 Graph를 활용해 풀어보자. 🔥
해당 문제는 고득점 kit의 가장 먼 노드 문제입니다. 문제는 여기 클릭해서 확인해주세요! (문제 저작권 보호차원 링크로 공유드립니다😟)
🖇 소스코드에 마우스를 올리고 copy 버튼을 누를 경우 더 쉽게 복사할 수 있습니다!
궁금한 점, 보안점 남겨주시면 성실히 답변하겠습니다. 😁
+ 감상평 댓글로 남겨주시면 힘이됩니다. 🙇
풀이
해당 문제는 가장 멀리 떨어진 노드의 갯수 를 구하는 문제이다.
본인은 해당 문제를 Graph 와 BFS를 통해 해결하였다. Graph로 연결된 노드들을 하나씩 탐색하며 가장 먼 노드를 찾는 방식으로 풀었다. 모든 경로를 탐색해야하고, 주어진 조건 상 최단 경로로 가장 먼 노드를 찾아야하기 때문에, BFS를 활용해서 풀었다.
문제 접근 과정
해당 문제를 풀기 위해서는 graph 만들기, BFS 탐색 2가지를 알면 쉽게 풀 수 있다.
아래의 그림을 보자.
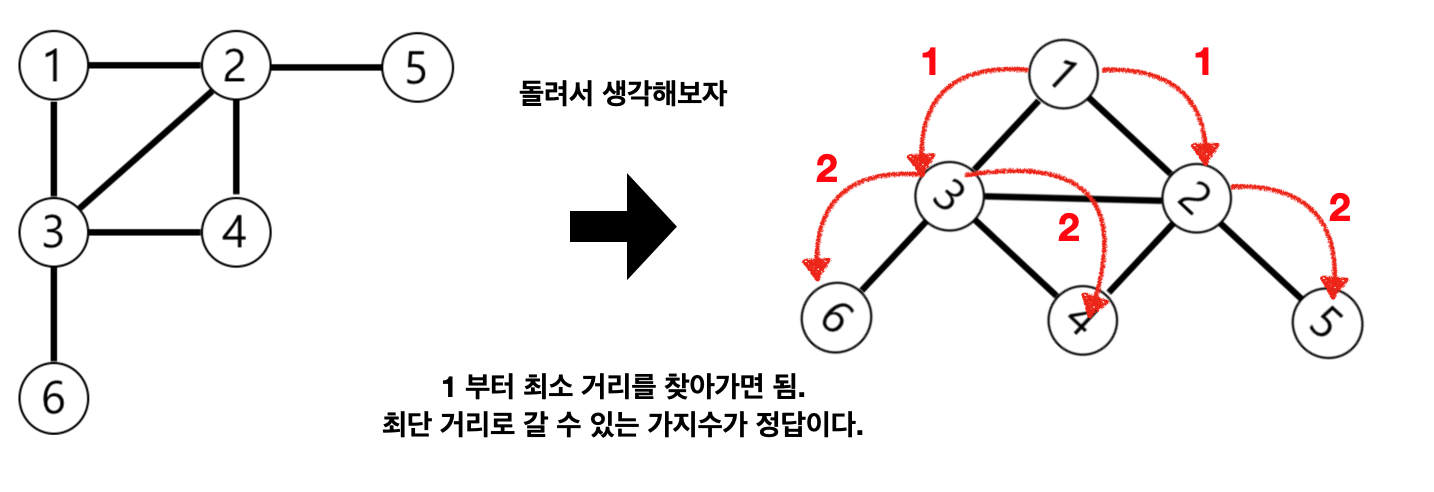
해당 문제의 그래프를 옆으로 살짝 돌려보자. 그럼 1 부터 가장 먼노드 까지 탐색을 해야하는 방향이 보일 것이다. 그림 기반으로 생각했을 때 풀이는 단순해 진다.
- 양방향 그래프 만들기
- 1 부터 BFS 탐색
- 가장 먼 노드 갯수 파악
1️⃣ 양방향 그래프 만들기
그래프를 만들기 위한 방법은 인접행렬과 인접 리스트 두 가지이다. 아래의 그림을 보자. 해당 그림은 여기 를 통해 가져온 그림이다. 설명도 꽤 잘나와있다.
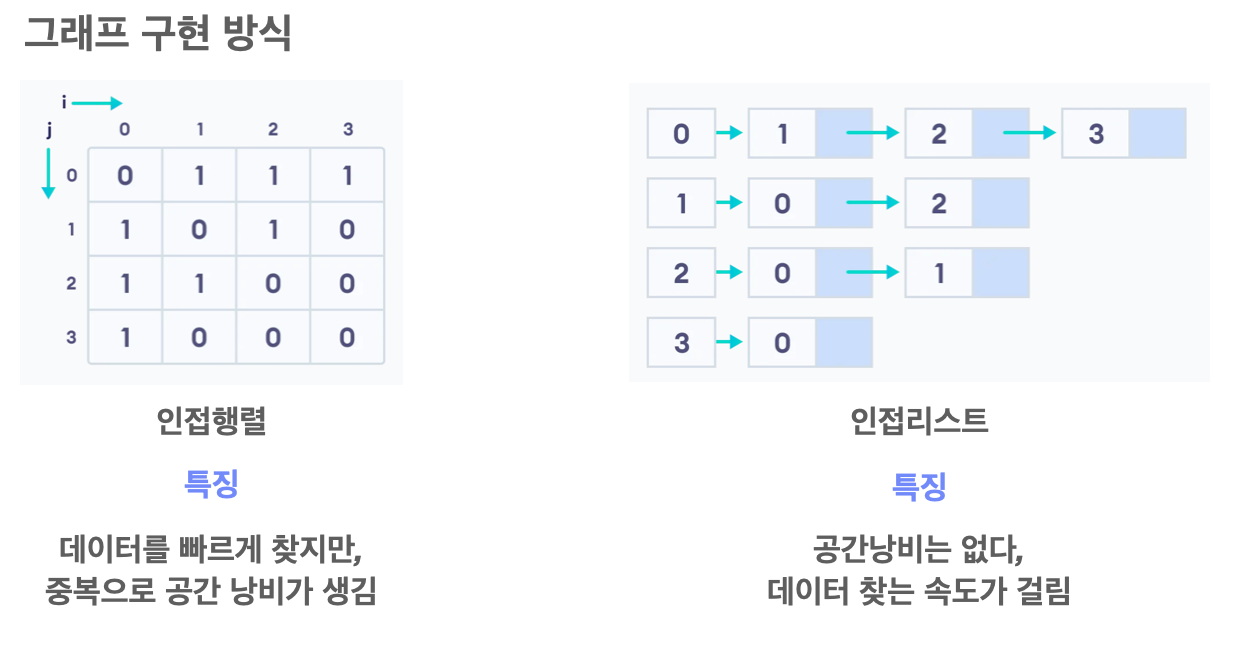
그래프를 만드는 방법은 행렬을 이용하는 방법과 리스트를 이용하는 방법이있다. 해당 문제에서 node를 2만개를 사용한다고 하니 행렬을 사용하면 공간낭비가 심할 것 같아 본인은 리스트를 사용하기로 한다. 리스트를 구현하는 방법은 간단하다. 아래 코드에서도 나오겠지만, 자세한 소스코드 위치를 보고 싶다면 Appendix 부분을 참고 하자. 간단하게 설명하자면, solution 함수 에서 2차원 vector를 구성한다. 이후 인자로 전달 받는 간선들을 list화 시켜준다. 여기서 중요한점이 해당 문제는 양방향 이라는 것이다. 양방향으로 구현 하는 부분도 유심히 보기 바란다.
2️⃣ 1 부터 BFS 탐색하기
위의 그래프를 만들었다면, BFS를 활용한 탐색을 시작하면 된다. BFS의 중요한 자료구조는 Queue 이다. 노드를 방문할 때마다 해당 노드에 인접해 있는 부분들을 Queue 집어 넣는다. 만약 Queue에 값이 남아 있을 경우 첫 번째 요소를 Pop 시켜 해당 노드를 방문한다.
Queue가 완료 될 때 까지 반복한다.
노드에 방문한 후, 1부터 현재 노드까지 오는 거리를 계산해 배열에 다 저장해둔다. 본인은 일반 배열이 아닌 vector를 사용했다. 일반 배열을 사용해도 된다. 하지만, 뒷 부분에 가장 먼 노드의 개수를 파악할 때 효율적 접근을 위해 vector를 사용하고자 한다.
추가로 중요한 자료구조가 visisted 배열이다. 아무래도 양방향이다보니 역으로 순회할 수 있는 경우의 수가 생길 수도 있다. 따라서, 방문 했을 경우 해당 배열을 true로 변경해주고, 갈 수 있는 가장 최단 거리를 계속해서 구해나 간다.
3️⃣ 최단 경로로 갈 수 있는 갯수 파악
2️⃣ 의 방법을 통해, 시작점인 1 부터 존재하는 노드 까지의 거리를 구해 vector에 저장해 두었다. 1 부터 가장 멀리 갈 수 있는 노드의 개수를 파악하는 문제임으로, 우리는 이전에 저장해 둔 vector에 가장 긴 거리를 파악하면 된다.
본인은 우선, sort()를 활용해 greater<int>기준 즉, 내림 차순 기준으로 정렬하였다. 가장 첫번째 요소 값이 가장 큰 값이라고 가정하고, 해당 값과 동일한 값들이 있는지를 파악해 갯수를 출력해 문제를 해결하였다.
소스코드
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
int solution(int n, vector<vector<int>> edge) {
vector<vector<int>> graph(n+1);
vector<int> counts(n+1, 0);
vector<bool> visited(n+1, false);
queue<int> queue;
int answer = 0;
for (int i = 0; i < edge.size(); i++) {
graph[edge[i][0]].push_back(edge[i][1]);
graph[edge[i][1]].push_back(edge[i][0]);
}
queue.push(1);
visited[1] = true;
while(!queue.empty()) {
int node = queue.front();
queue.pop();
for (int i = 0; i < graph[node].size(); i++) {
if (!visited[graph[node][i]]) {
int currentCount = counts[node] + 1;
visited[graph[node][i]] = true;
counts[graph[node][i]] = currentCount;
queue.push(graph[node][i]);
}
}
}
sort(counts.begin(), counts.end(), greater<int>());
for (auto cnt : counts) {
if (counts[0] != cnt) break;
answer++;
}
return answer;
}
Appendix
부분 부분 주석을 남겨놓았다. 주석코드와 함께 소스코드를 보고 이해하도록 하자.
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
/**************
* 제한 사항
* 노드의 개수 n은 2 이상 20,000 이하입니다.
* 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
* vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
***************/
int solution(int n, vector<vector<int>> edge) {
// 2차원 그래프만들기 위한 배열
vector<vector<int>> graph(n+1);
// counter를 위한 배열
vector<int> counts(n+1, 0);
// visited 배열
vector<bool> visited(n+1, false);
// BFS를 위한 Queue
queue<int> queue;
int answer = 0;
/* 1번 부분 */
// 인접 리스트 기반 그래프 생성하는 부분
for (int i = 0; i < edge.size(); i++) {
// 양방향 그래프라 시작점과 끝점을 번갈아 가며 연결해준다.
graph[edge[i][0]].push_back(edge[i][1]);
graph[edge[i][1]].push_back(edge[i][0]);
}
queue.push(1);
visited[1] = true;
/* 2번 부분 */
// BFS
while(!queue.empty()) {
int node = queue.front();
queue.pop();
for (int i = 0; i < graph[node].size(); i++) {
// 최단거리를 위해 방문 유무를 검사한다.
if (!visited[graph[node][i]]) {
// 거리를 하나 증가시킨다.
int currentCount = counts[node] + 1;
visited[graph[node][i]] = true;
// 방문 후 카운트 증가하는 부분
counts[graph[node][i]] = currentCount;
queue.push(graph[node][i]);
}
}
}
/* 3번 부분 */
// 정렬해 가장 먼 노드의 개수를 구하는 부분
sort(counts.begin(), counts.end(), greater<int>());
for (auto cnt : counts) {
if (counts[0] != cnt) break;
answer++;
}
return answer;
}
처음에 그래프 만드는 부분을 떠올리지 못해 많이 해맸던 것 같다. 그래프 만드는 부분들 기억하고 외우도록 하자.

